Mandel's problem

The original Mandel's problem considered a rectangular soil sample subject to a constant force (vertical stress) at its top where the fluid and the solid were incompressible. Here we consider the extension of the Mandel's problem in which the fluid and solid particles are compressible. This extension to the Mandel's problem was first introduced by Cheng and Detournay (1988).

Setup

A rectangular soil sample (width $var element = document.getElementById("moose-equation-cb23fedb-5737-429e-abb0-82fa7815bc13");katex.render("2a", element, {displayMode:false,throwOnError:false});$ and height $var element = document.getElementById("moose-equation-e19092db-d8ac-42a4-b476-82d2fdb4904a");katex.render("b", element, {displayMode:false,throwOnError:false});$ ) is subject to a vertical stress $var element = document.getElementById("moose-equation-4cfb3855-b779-43e9-99cb-8fbc75750158");katex.render("F", element, {displayMode:false,throwOnError:false});$ at its top through a rigid and frictionless plate of length $var element = document.getElementById("moose-equation-4d621034-2498-4863-b947-93039f126fb1");katex.render("2a", element, {displayMode:false,throwOnError:false});$ . The lateral boundary of the sample are drained and deformation is in-plane. At $var element = document.getElementById("moose-equation-a26d465f-e2a0-4395-84d7-eda6e01b0007");katex.render("t = 0", element, {displayMode:false,throwOnError:false});$ the vertical force of magnitude $var element = document.getElementById("moose-equation-2051c745-2ee6-4333-a31a-e508bc881924");katex.render("F", element, {displayMode:false,throwOnError:false});$ is applied and fluid pressure increases due to poroelastic effect. It then drains out of the lateral boundary over time. See a sketch of this setup in Figure 1.

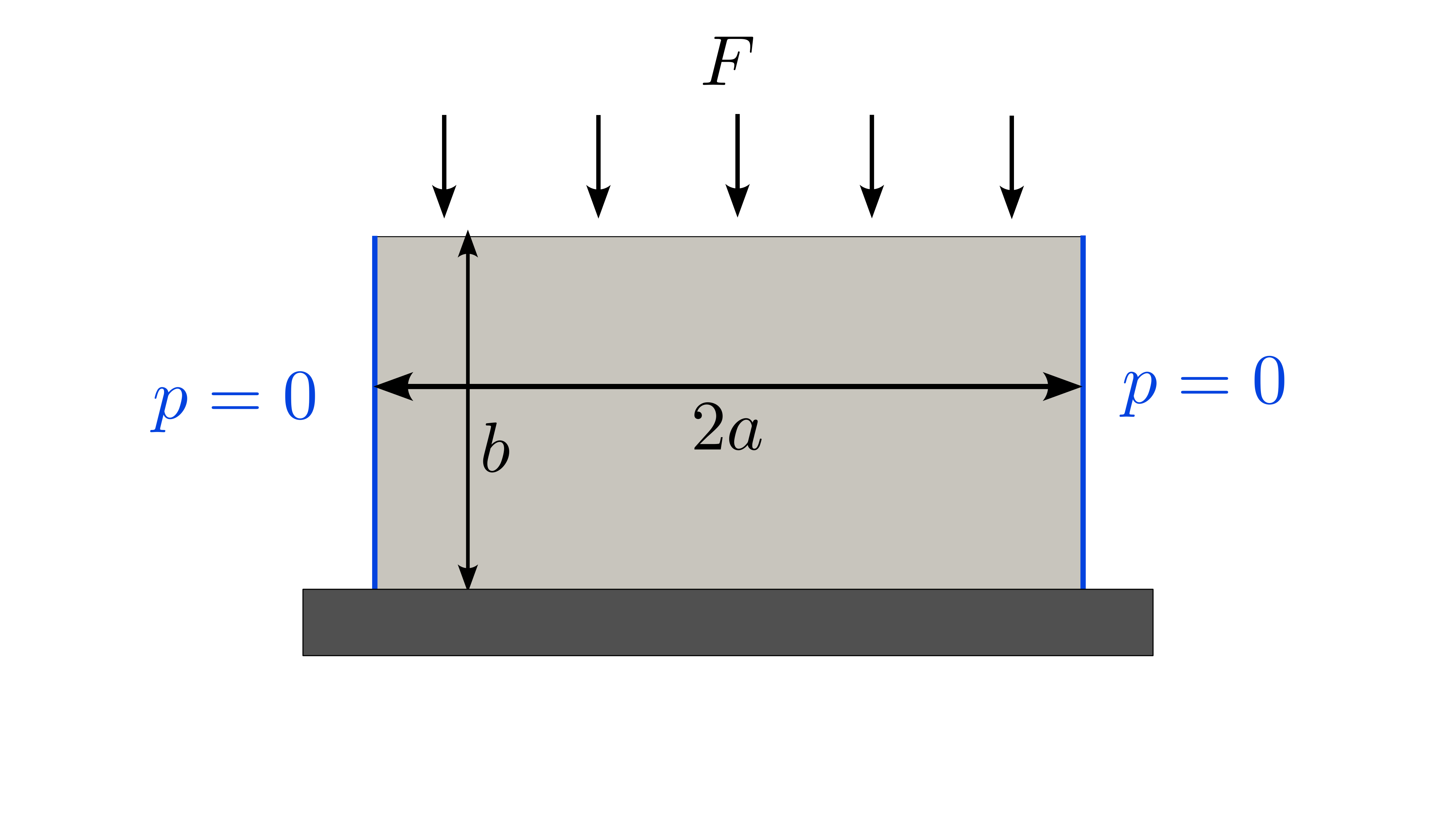
Figure 1: Setup for the Mandel's problem.

Parameters

Table 1: List of parameters used for the Mandel's problem.

Symbol	Value	Unit	Name
$var element = document.getElementById("moose-equation-c4551ccc-c319-42eb-aab7-d1633384c987");katex.render("K", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-535352a9-837d-4c09-af4b-99963aa126a7");katex.render("1.0", element, {displayMode:false,throwOnError:false});$	Pa	Bulk modulus
$var element = document.getElementById("moose-equation-47790e1c-ee80-4896-bba0-05cc913fd705");katex.render("\\nu", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-7c7799ad-5a27-4278-bc2a-cfb5f1c822f4");katex.render("0.25", element, {displayMode:false,throwOnError:false});$	-	Poisson's ratio
$var element = document.getElementById("moose-equation-44e8fbf2-b0cc-4ed2-9bc8-1208e1b685a3");katex.render("\\alpha", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-bee16c61-7f82-4fbc-8eea-567a6cc457ed");katex.render("0.6", element, {displayMode:false,throwOnError:false});$	-	Biot's poroelastic coefficient
$var element = document.getElementById("moose-equation-9c52c84e-c2c3-4a91-ac58-62079d4e69f1");katex.render("k", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-91c60fb4-c3d5-4760-989c-b37e831f98cf");katex.render("1.5", element, {displayMode:false,throwOnError:false});$	m $var element = document.getElementById("moose-equation-9cb70633-ff95-4451-a828-bf73d0b2031b");katex.render("^{2}", element, {displayMode:false,throwOnError:false});$	Permeability
$var element = document.getElementById("moose-equation-22dee86e-31f2-4144-9e11-4678f24c6d6c");katex.render("\\mu", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-026c4211-ee58-4372-a2eb-cfbbf4d7e7bc");katex.render("1.0", element, {displayMode:false,throwOnError:false});$	Pa s	Fluid viscosity
$var element = document.getElementById("moose-equation-206f2c18-95fd-46d0-9049-485c1a45d684");katex.render("\\phi", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-fb7a2685-1674-455d-b293-ca7e9fe9f436");katex.render("0.1", element, {displayMode:false,throwOnError:false});$	-	Porosity
$var element = document.getElementById("moose-equation-797c50ee-eef9-4eb8-b12e-9bf0b12ecd00");katex.render("K_{f}", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-e2799a1d-3246-4a1c-ad7b-0f2fff6d1411");katex.render("8.0", element, {displayMode:false,throwOnError:false});$	Pa	Fluid bulk modulus
$var element = document.getElementById("moose-equation-c39a61d2-f40e-47fa-bee3-d33c334c5672");katex.render("F", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-8288dc6d-2414-4c98-9e7a-e1e0b07bc4c4");katex.render("1.0", element, {displayMode:false,throwOnError:false});$	Pa	Applied force

Here are definitions of some poroelastic parameters:

Solid bulk modulus: $var element = document.getElementById("moose-equation-49521a3e-eb54-4efb-beac-41b49558adec");katex.render("K_{s} = \\frac{K}{1 - \\alpha}", element, {displayMode:false,throwOnError:false});$
Storage coefficient: $var element = document.getElementById("moose-equation-8f47c2df-e44e-4a40-a29d-6820d2a73f6d");katex.render("S = \\frac{\\phi}{K_{f}} + \\frac{\\alpha - \\phi}{K_{s}}", element, {displayMode:false,throwOnError:false});$
Undrained bulk modulus: $var element = document.getElementById("moose-equation-864d978c-3ff2-46e7-aa85-c6c10891984a");katex.render("K_{u} = \\frac{\\alpha^{2} + K S}{S}", element, {displayMode:false,throwOnError:false});$
Skempton's coefficient: $var element = document.getElementById("moose-equation-589196d8-edb3-44cc-80aa-117da18406ff");katex.render("B = \\frac{\\alpha}{\\alpha^{2} + K S}", element, {displayMode:false,throwOnError:false});$
Undrained Poisson's ratio: $var element = document.getElementById("moose-equation-32bf6da3-50fa-4831-bee1-f8cf01a32d05");katex.render("\\nu_{u} = \\frac{1}{2} \\frac{K_{u} - K \\frac{1 - 2 \\nu}{1 + \\nu}}{K_{u} + K \\frac{1 - 2 \\nu}{2 \\left(1 + \\nu\\right)}}", element, {displayMode:false,throwOnError:false});$
Consolidation coefficient: $var element = document.getElementById("moose-equation-f56bb24c-73ba-4773-bc1e-61f89bc5ad20");katex.render("c_{v} = \\frac{k}{\\mu} \\frac{B^{2} K \\left(1 - 2\\nu\\right) \\left(1 - \\nu\\right) {\\left(1 + \\nu_{u}\\right)}^2}{3 \\left(1 + \\nu\\right) \\left(1 - \\nu_{u}\\right) \\left(\\nu_{u} - \\nu\\right)}", element, {displayMode:false,throwOnError:false});$

Solutions

The solutions for this problem are given by Cheng and Detournay (1988). The fluid pressure solution is given as:

(1)var element = document.getElementById("moose-equation-09df00ab-38cc-470c-a9e4-0247e874d869");katex.render("p\\left(x, t\\right) = \\frac{2 p_{0}}{a} \\sum_{j=1}^{N} \\frac{\\sin\\xi_{j}}{\\xi_{j} - \\sin \\xi_{j} \\cos \\xi_{j}} \\left(\\cos\\left(\\xi_{j} \\frac{x}{a}\\right) - \\cos \\xi_{j}\\right) \\exp \\left(-\\xi_{j}^{2} \\frac{c_{v} t}{a^{2}}\\right),", element, {displayMode:true,throwOnError:false});

where:

var element = document.getElementById("moose-equation-a39e5e95-177c-47e3-873e-6d5f3753571b");katex.render("p_{0} = \\frac{F B \\left(1 + \\nu_{u}\\right)}{3 a}.", element, {displayMode:true,throwOnError:false});

The vertical displacement solution is given as:

(2)var element = document.getElementById("moose-equation-ce7c8bf4-4018-43af-89b0-5c3d6febd988");katex.render("u_{y}\\left(t\\right) = u_{y}\\left(+\\infty\\right) - 2 u_{y}\\left(0\\right) \\frac{\\sin \\xi_{j} \\cos \\xi_{j}}{\\xi_{j} - \\sin \\xi_{j} \\cos \\xi_{j}} \\exp \\left(-\\xi_{j}^{2} \\frac{c_{v} t}{a^{2}}\\right),", element, {displayMode:true,throwOnError:false});

where

var element = document.getElementById("moose-equation-129f49af-a3be-450c-9821-9680ec3dce3f");katex.render("u_{y}\\left(+\\infty\\right) = - \\frac{F \\left(1 - \\nu^{2}\\right)}{3 K \\left(1 - 2\\nu\\right)} \\frac{b}{a},", element, {displayMode:true,throwOnError:false});

and

var element = document.getElementById("moose-equation-4fcc365d-bf8a-4950-8478-b94cdef4bd61");katex.render("u_{y}\\left(0\\right) = - \\frac{F \\left(1 - \\nu_{u}\\right) \\left(1 + \\nu\\right)}{3 K \\left(1 - 2\\nu\\right)} \\frac{b}{a}.", element, {displayMode:true,throwOnError:false});

The coefficient $var element = document.getElementById("moose-equation-655a1a5e-e162-4ca3-873a-bfc7de467e8a");katex.render("\\xi_{j}", element, {displayMode:false,throwOnError:false});$ are the roots verifying the following equations:

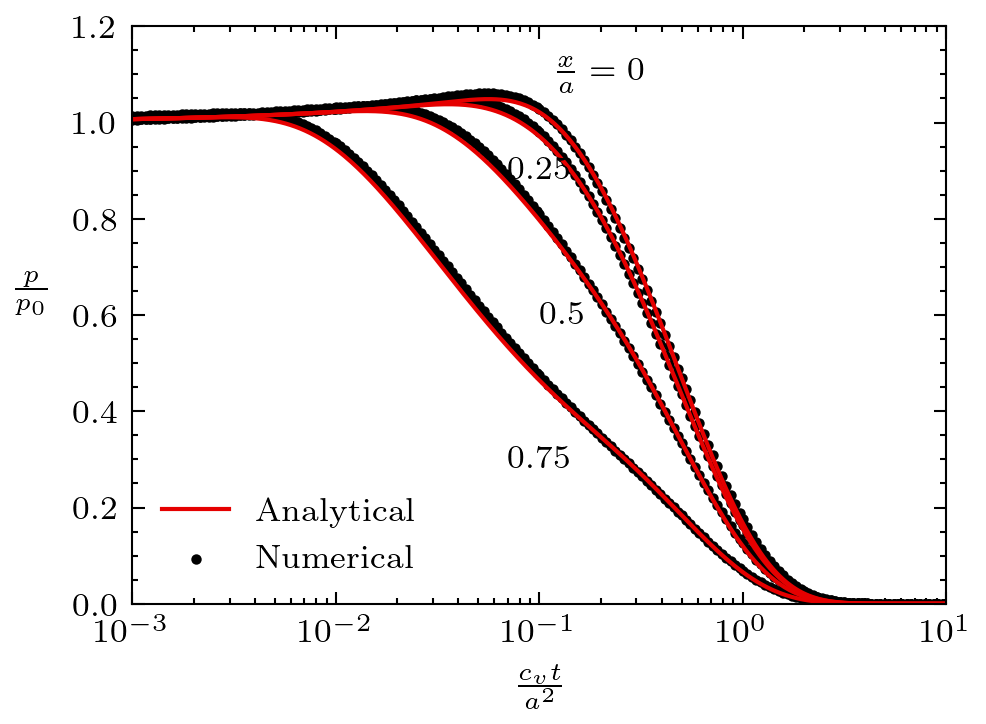
(3)var element = document.getElementById("moose-equation-c4ffcac3-655e-4007-a5f9-b749912def86");katex.render("\\tan \\xi_{j} = \\frac{1 - \\nu}{\\nu_{u} - \\nu} \\xi_{j}.", element, {displayMode:true,throwOnError:false});

Figure 2: Fluid pressure solution for the Mandel's problem.

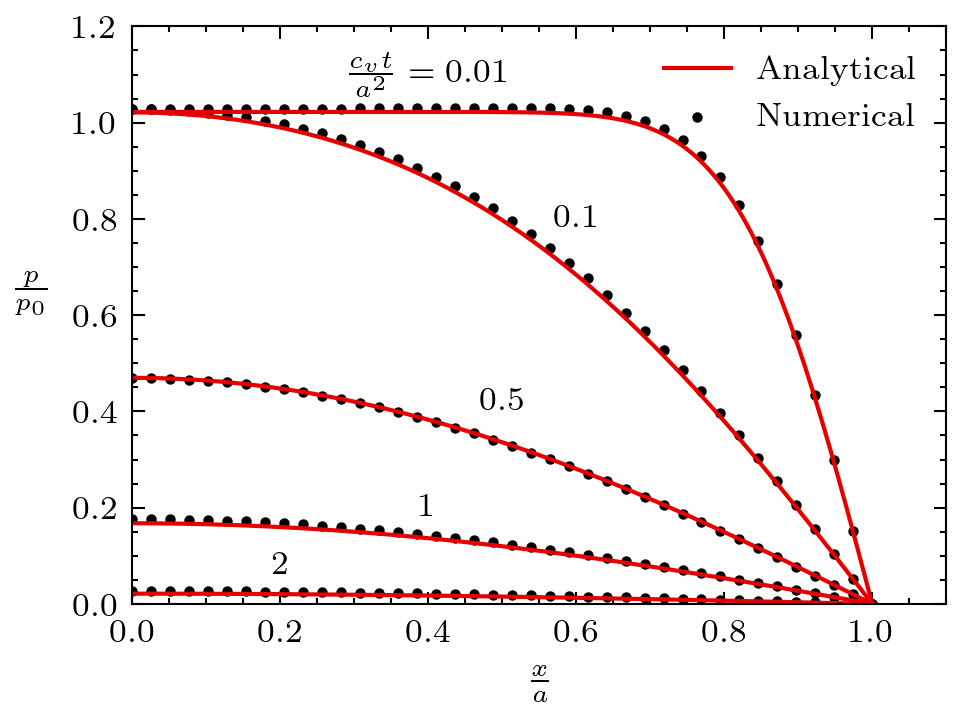
Figure 3: Fluid pressure solution for the Mandel's problem.

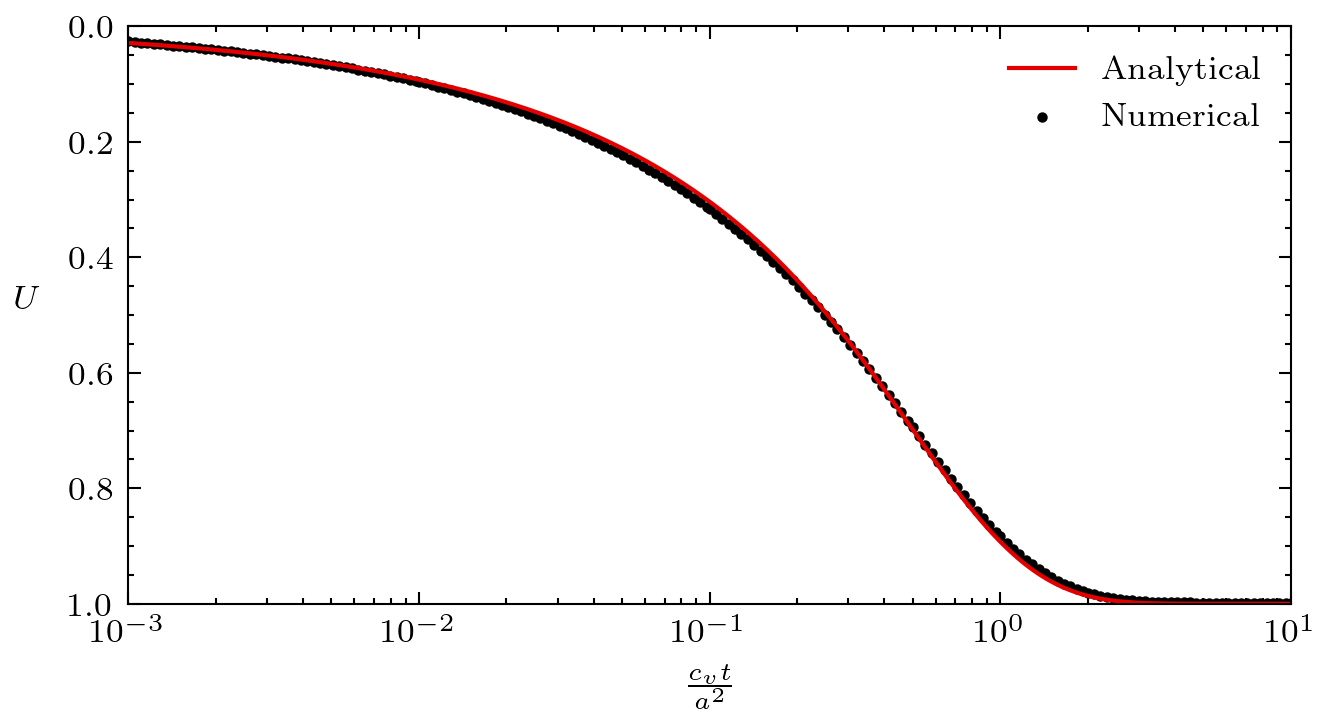
Figure 4: Consolidation solution for the Mandel's problem.

Complete Source Files

mandel.i

References

Alexander H.‐D. Cheng and Emmanuel Detournay. A direct boundary element method for plane strain poroelasticity. International Journal for Numerical and Analytical Methods in Geomechanics, 12(5):551–572, 1988. doi:10.1002/nag.1610120508.

@article{Cheng1988,
    author = "Cheng, Alexander H.‐D. and Detournay, Emmanuel",
    year = "1988",
    title = "{A direct boundary element method for plane strain poroelasticity}",
    journal = "International Journal for Numerical and Analytical Methods in Geomechanics",
    issn = "0363-9061",
    doi = "10.1002/nag.1610120508",
    pages = "551--572",
    number = "5",
    volume = "12"
}

Terzaghi s consoli. . .Cryer s problem

Setup
Parameters
Solutions
Complete Source Files
References