Cryer's problem

The Cryer's problem consists in a spherical soil sample subject to external load with the surface of the sphere considered drained. The fluid pressure increases within the sphere shortly after the external load is applied with its maximum value at the center of the sphere and then progressively decreases as the over pressure drain via the external surface. The original Cryer problem was somewhat simpler than this problem as we consider here both the fluid and solid particles to be compressible.

Setup

The sphere of radius $var element = document.getElementById("moose-equation-dfb69f90-6473-4196-aa33-bc89888c32ee");katex.render("a", element, {displayMode:false,throwOnError:false});$ is subject at time $var element = document.getElementById("moose-equation-c5f86306-2880-4053-9d62-ace2cf7c4ce5");katex.render("t = 0", element, {displayMode:false,throwOnError:false});$ to an external force of magnitude $var element = document.getElementById("moose-equation-52ffca5f-495e-40f0-9777-e2703aebd936");katex.render("F", element, {displayMode:false,throwOnError:false});$ normal to its external surface. The external surface is drained. A sketch of the problem setup can be found in Figure 1. Due to symmetry of the problem, we model only an eighth of the sphere.

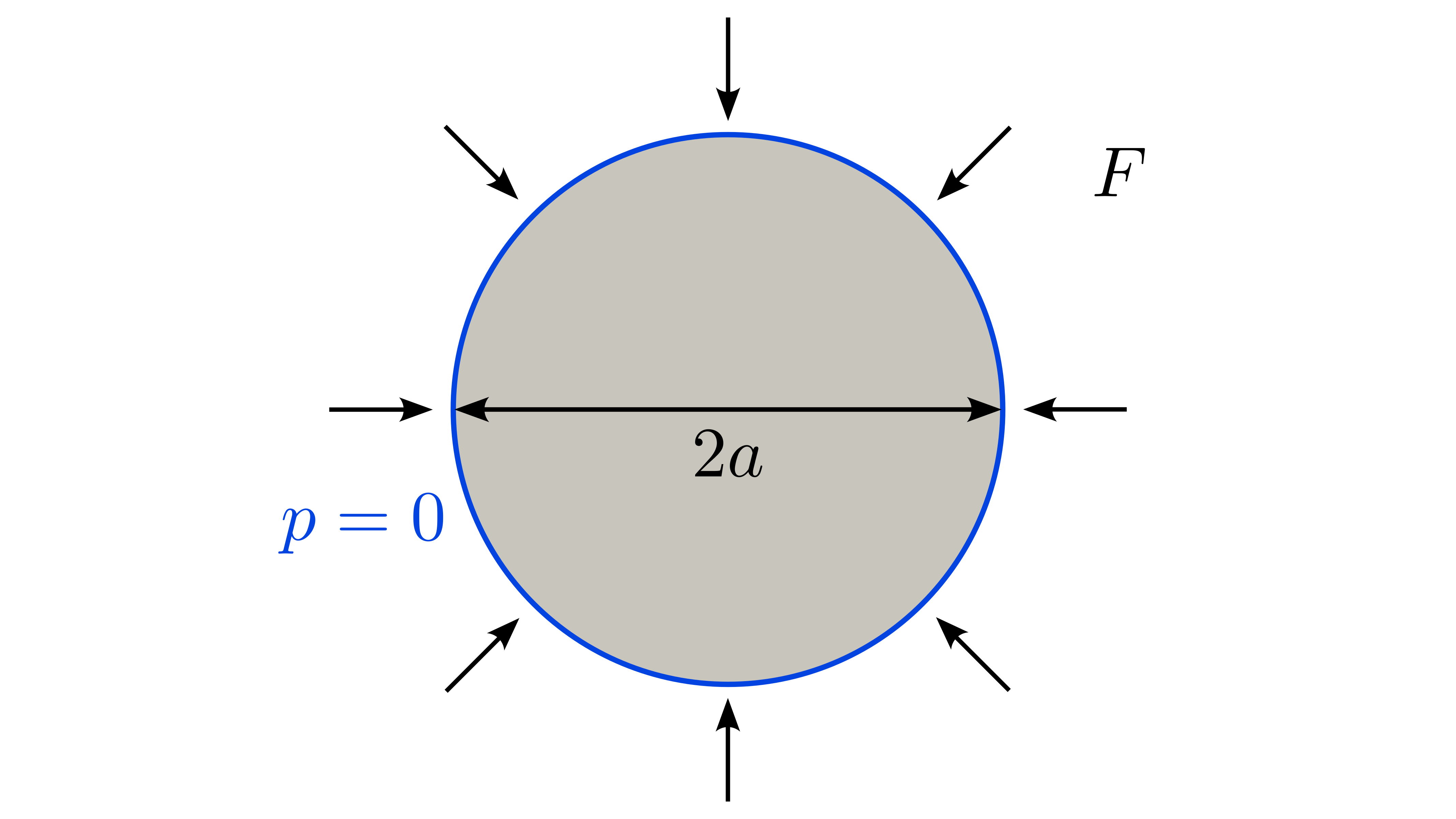
Figure 1: Setup for the Cryer's problem.

Parameters

Table 1: List of parameters used for the Cryer's problem.

Symbol	Value	Unit	Name
$var element = document.getElementById("moose-equation-fdfa35b8-c8fe-46c0-99f0-61fde1c3a3dd");katex.render("K", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-1beac1e3-ffff-42c6-a22f-c8b3b28329c9");katex.render("1.0", element, {displayMode:false,throwOnError:false});$	Pa	Bulk modulus
$var element = document.getElementById("moose-equation-4b1fdbf8-9451-4b51-a2f6-af583905d0f8");katex.render("\\nu", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-81836d1e-0813-4bd3-8544-f841b6ddbbb3");katex.render("0.25", element, {displayMode:false,throwOnError:false});$	-	Poisson's ratio
$var element = document.getElementById("moose-equation-686ba1c4-a94e-4e30-a1f3-2b05f324a6cd");katex.render("\\alpha", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-7768d0d2-d1a7-4af4-8ab7-5c01c907e8b5");katex.render("0.6", element, {displayMode:false,throwOnError:false});$	-	Biot's poroelastic coefficient
$var element = document.getElementById("moose-equation-23ecd617-6f80-43cd-a64d-ca753f1cc904");katex.render("k", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-35548df3-c470-41c9-bb0e-90d729d4b028");katex.render("1.5", element, {displayMode:false,throwOnError:false});$	m $var element = document.getElementById("moose-equation-b001dcbb-4234-464d-9a33-e95bdbe37a85");katex.render("^{2}", element, {displayMode:false,throwOnError:false});$	Permeability
$var element = document.getElementById("moose-equation-78c25f9b-3d18-448f-8c88-c716ef3f3fb9");katex.render("\\mu", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-8e3df0e4-cccf-44a6-870c-6474c18fb59d");katex.render("1.0", element, {displayMode:false,throwOnError:false});$	Pa s	Fluid viscosity
$var element = document.getElementById("moose-equation-10f08dee-81f9-467c-a369-5071e4ecb514");katex.render("\\phi", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-910ee770-0087-4000-b5e3-478139b9cf0a");katex.render("0.1", element, {displayMode:false,throwOnError:false});$	-	Porosity
$var element = document.getElementById("moose-equation-a7a22c9b-bf27-4b7d-b863-c78c740a54de");katex.render("K_{f}", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-d038c94a-54ad-4fa9-a9ce-b64145297370");katex.render("8.0", element, {displayMode:false,throwOnError:false});$	Pa	Fluid bulk modulus
$var element = document.getElementById("moose-equation-4f0d3ed2-f388-4eb6-9a8a-3c2491627dfe");katex.render("F", element, {displayMode:false,throwOnError:false});$	$var element = document.getElementById("moose-equation-19a82d25-2369-446a-b957-c7246d0d3400");katex.render("1.0", element, {displayMode:false,throwOnError:false});$	Pa	Applied force

Here are definitions of some poroelastic parameters:

Solid bulk modulus: $var element = document.getElementById("moose-equation-02484b9f-a05e-4075-9038-9ab7e9ed07b8");katex.render("K_{s} = \\frac{K}{1 - \\alpha}", element, {displayMode:false,throwOnError:false});$
Storage coefficient: $var element = document.getElementById("moose-equation-6148d3fa-1f49-460c-8954-f8d961efa8b2");katex.render("S = \\frac{\\phi}{K_{f}} + \\frac{\\alpha - \\phi}{K_{s}}", element, {displayMode:false,throwOnError:false});$
Unnamed parameter $var element = document.getElementById("moose-equation-1024a4bc-1cec-4774-912a-9ab3be95a858");katex.render("m = \\frac{1 - \\nu}{1 - 2 \\nu}", element, {displayMode:false,throwOnError:false});$
Unnamed parameter $var element = document.getElementById("moose-equation-136a85ce-74f6-4d38-9d76-60f392d5b598");katex.render("\\eta = m \\left(1 + \\frac{KS}{\\alpha^{2}}\\right)", element, {displayMode:false,throwOnError:false});$
Consolidation coefficient: $var element = document.getElementById("moose-equation-4a2c258a-9ac1-4aaa-af6d-555a31749fca");katex.render("c_{v} = \\frac{k}{\\mu} \\frac{K + \\frac{4}{3} G}{\\alpha^{2} + S\\left(K + \\frac{4}{3}G\\right)}", element, {displayMode:false,throwOnError:false});$

Solutions

Verruijt (2016) gives the full solution of this problem using Laplace transforms. Here, we only look at the evolution over time of the fluid pressure at the center of the sphere noted $var element = document.getElementById("moose-equation-8e334e91-f252-4e58-b72b-339fc260a04f");katex.render("p_{c}", element, {displayMode:false,throwOnError:false});$ which is given as:

var element = document.getElementById("moose-equation-f035d0a7-403a-4d11-8382-425ce7f663f4");katex.render("\\frac{p_{c}\\left(t\\right)}{p_{0}} = \\eta \\sum_{j=1}^{+\\infty} \\frac{\\sin \\xi_{j} - \\xi_{j}}{\\left(\\eta - 1\\right) \\sin \\xi_{j} + \\frac{\\eta}{2} \\xi_{j} \\cos \\xi_{j}} \\exp\\left(- \\xi_{j}^{2} \\frac{c_{v}t}{a^{2}}\\right),", element, {displayMode:true,throwOnError:false});

where $var element = document.getElementById("moose-equation-ecdf7419-f274-4a17-9734-7da7aa14cb08");katex.render("p_{0}", element, {displayMode:false,throwOnError:false});$ is given as:

var element = document.getElementById("moose-equation-12b35f8b-c626-4a41-8f0a-a68b9d990770");katex.render("p_{0} = \\frac{F}{\\alpha \\left(1 + \\frac{KS}{\\alpha^{2}}\\right)}.", element, {displayMode:true,throwOnError:false});

The coefficients $var element = document.getElementById("moose-equation-5ad5a624-783d-49c0-875b-76849d6e1881");katex.render("\\xi_{j}", element, {displayMode:false,throwOnError:false});$ are the positive roots of the equation:

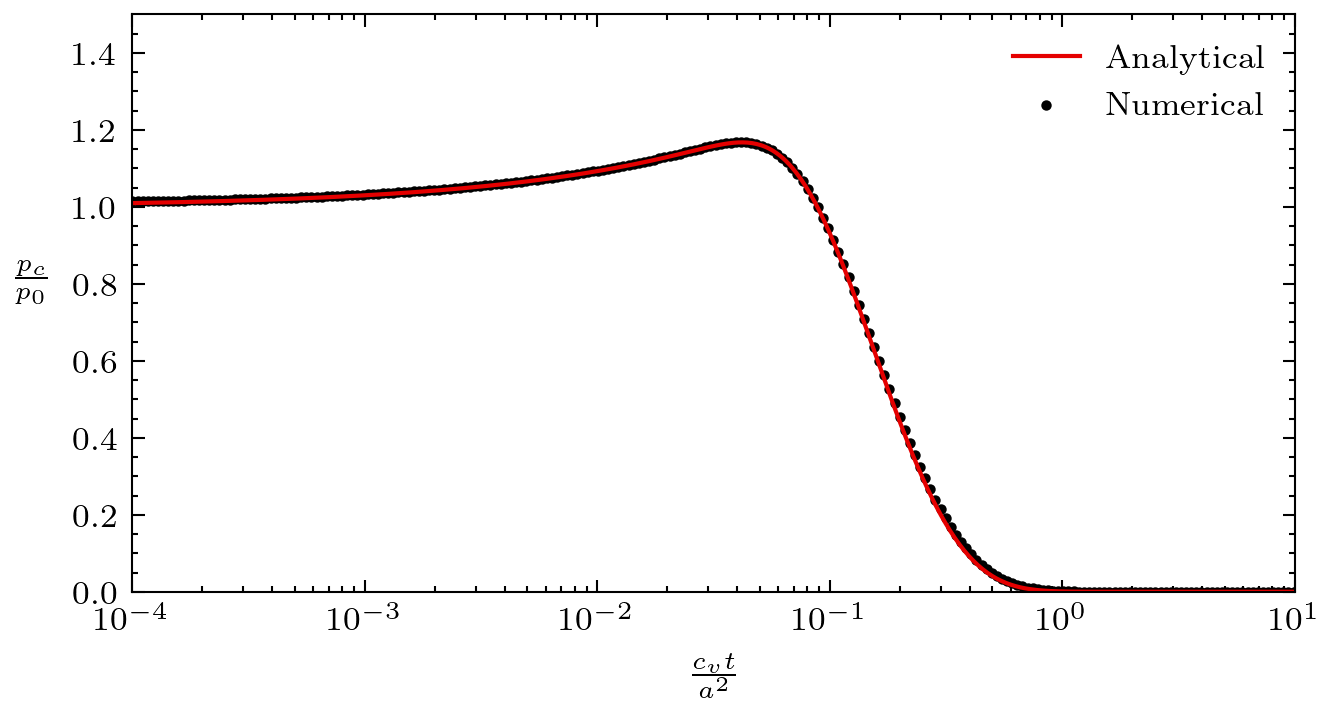
var element = document.getElementById("moose-equation-f1cc9bce-f635-4e0d-9cff-cdf50bf43236");katex.render("\\left(1 - \\eta \\frac{\\xi_{j}^{2}}{2}\\right) \\tan \\xi_{j} = \\xi_{j}.", element, {displayMode:true,throwOnError:false});

Figure 2: Fluid pressure solution for the Cryer's problem.

Complete Source Files

mandel.i

References

Arnold Verruijt. Theory and problems of poroelasticity. Delft University of Technology, 2016.

@book{Verruijt2016,
    author = "Verruijt, Arnold",
    editor = "Verruijt, Arnold",
    publisher = "Delft University of Technology",
    title = "{Theory and problems of poroelasticity}",
    year = "2016"
}

Mandel s problem

Setup
Parameters
Solutions
Complete Source Files
References